This term is used in conjunction with, and therefore often confused with, others, such as Concept drift, Covariate shift and even Label shift. To explain the differences between all these, we first define the following mathematical notations. The input data set to the model is called X, and consequently the output data or estimations are called Y. The conditional probability of obtaining an output, Y, based on the input X is denoted by P(X|Y).

In this article, I'm going to focus my attention on defining data drift and concept drift, since they are frequently used interchangeably.

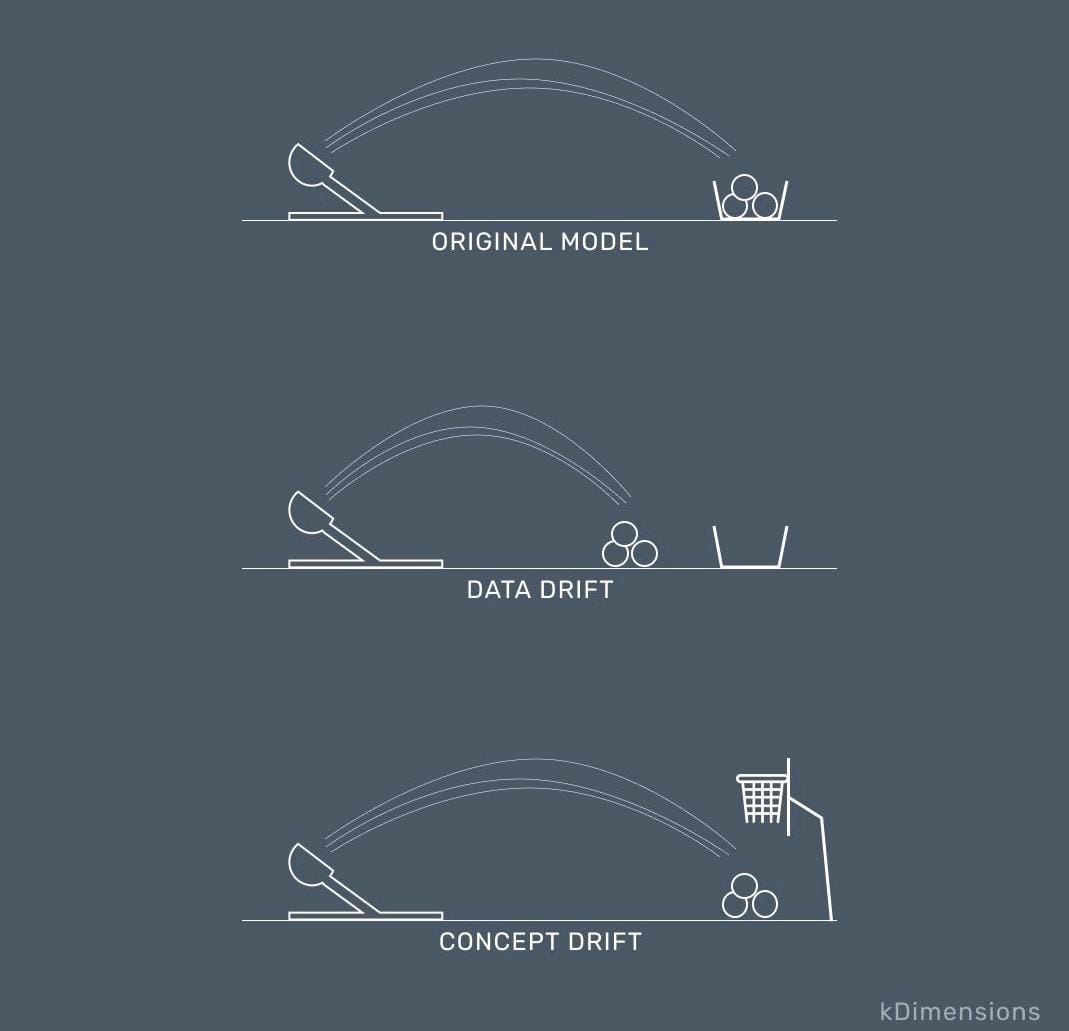
DATA DRIFT

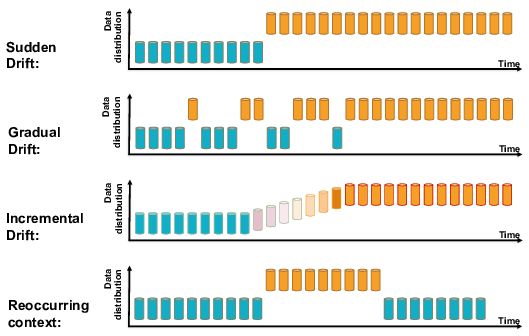
Data drift happens when a model's input data changes in ways that weren't seen during training. This change can be gradual, sudden or stationary. This is   P(Y|X)_train = P(Y|X)_test However  P(X)_train ≠ P(X)_test.

This is, a model responds by generating the same output for the same input. The problem is that the way in which the input data behaves changes in ways unseen in its training phase, resulting in an erroneous prediction of the output variable.

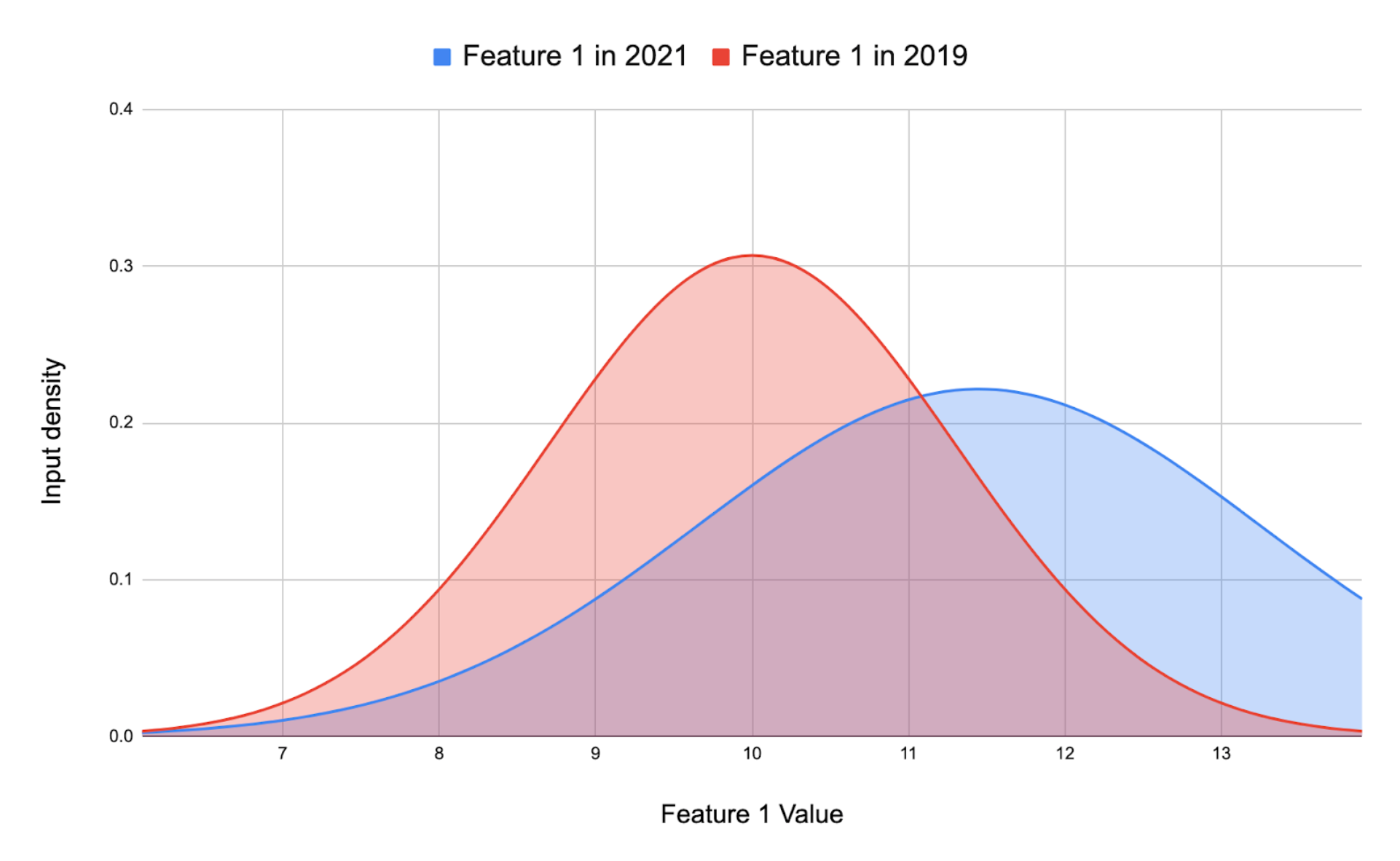
Let's imagine that a bus detector model has been developed. This model detects buses in a photo. The data set provided for the training of this model was full of images of line buses from a city. During the first stages of this model, the performance was superb, but as time passes, the old buses are gradually being replaced by new electric buses in the city. Now, the model makes a huge number of errors since it wasn't trained to detect those types of buses. This way, data drift made that model lose performance.

Herein lies the importance of monitoring and detecting this phenomenon in time.

The solution is easy and clear in this case, the model should be re-trained. But how much time has the model been working with a lower performance than required? And, what if we can't measure our model's performance?

The first option to mitigate the effects of data drift consists of a systematic retraining of the model. In this case, a lot of computational resources would be needed, without any improvement, which is not optimal. However, this technique mitigates the effects of data drift , which in some cases may be sufficient.

There is another way to deal with the problem, which is through a framework that monitors the input data. This is more sophisticated and better in the long run, but it requires constant monitoring of the data. However, fewer computational resources are used.

CONCEPT DRIFT

A model suffer concept drift when P(Y|X)_train ≠ P(Y|X)_test However  P(X)_train = P(X)_test .

That is, the input data behaves in the same way, following the same trend. However, the model's predictions worsen over time. The model's predictions get worse as time goes by.

Let's take as an example the development of a model that estimates the temperature inside of a cylinder inside of an engine. This model has many inputs, and its output is the variable temperature inside the cylinder.

In this case, the model works without any problems, and during its early stages, the predictions suggested by the model are correct.

Gradually, however, the cylinder begins to have small notches in its interior as well as an increasingly clogged intake and exhaust .

Although the variable to be predicted is the same and the input data follows the same trend as those used to train the model, the error in the temperature estimation becomes larger and larger. This is due to the fact that the model was trained on a system that has changed. A concept drift occurs in this type of situation.

Conclusion:

To sum up, data drift tends to be confused with other similar concepts, such as label shift, concept drift, or covariate shift. Although they are different concepts, they all have in common the fact that they are undesirable phenomena and therefore problems to control and, if they occur, to solve.